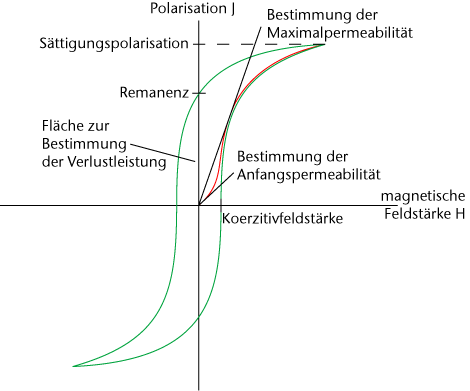
Soft magnetic materials can be found in many technical applications, such as transformers, small motors, transformers, filters, chokes or shielding. They are characterized by their magnetic properties. The characteristic values are the remagnetization losses, coercivity, magnetic polarization, saturation polarization, induction, permeability, susceptibility and remanence.
The diagram above shows how these typical magnetic parameters can be determined from the hysteresis curve of a magnetic material.
Depending on their area of application, the main focus is placed on one or more of the aforementioned magnetic parameters. In a transformer, for example, a high magnetic induction as well as a high permeability of the core material should be present at the same time, whereby the coercive field strength and the remagnetization losses should be as low as possible. Unfortunately, there is no soft magnetic material that fulfills these conditions, so that the best possible compromise must be sought.
Unfortunately, many magnetic characteristics are also dependent on the remagnetization frequency. Therefore, not all materials can be used in the same frequency range.
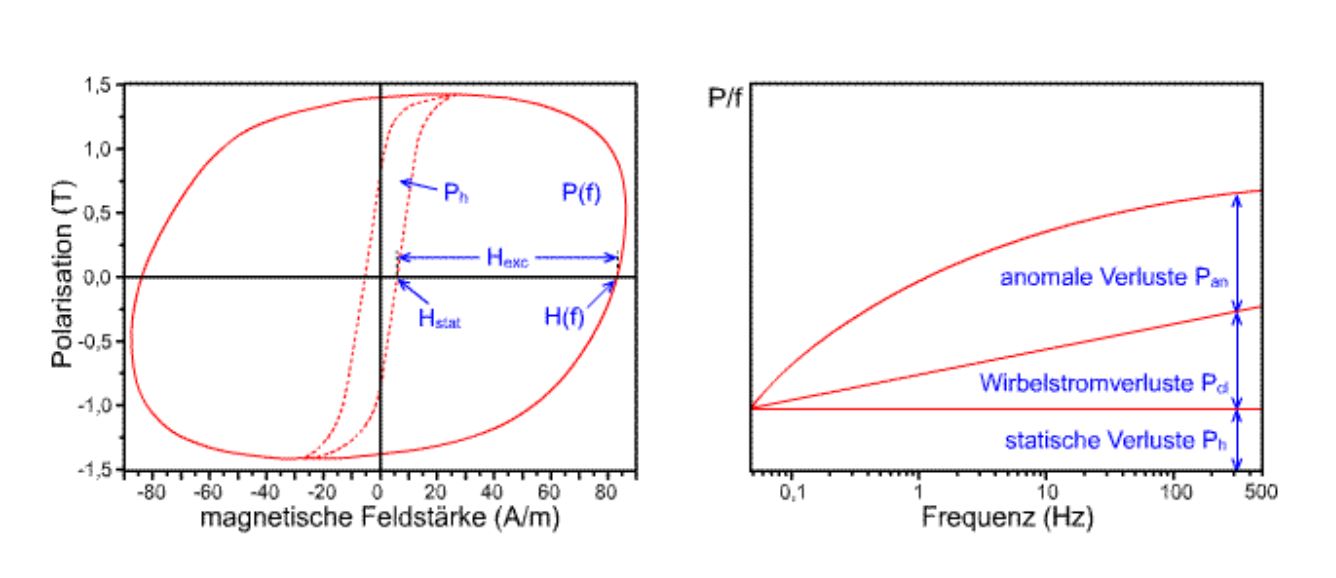
The figure on the right shows how the hysteresis loop has expanded at a significantly higher remagnetization frequency. The area enclosed by the hysteresis curve is a measure of the magnitude of the remagnetization losses in the magnetic material. The animation shows measured values obtained on grain-oriented iron-silicon electrical sheets for large transformers. Of course, a corresponding frequency dependence also applies to other magnetic materials.
The increase in remagnetization losses is shown in the right half of the image as a function of frequency. The demagnetization losses are divided into the staticPh, the classical eddy current losses Pcl and the anomalous demagnetization lossesPan. The static remagnetization losses are determined by material properties such as dislocation density, grain size, impurities, etc. The classical eddy current losses can be calculated from Maxwell's equations and are dependent on the shape of the induced signal, the sample geometry, the magnetic polarization, the remagnetization frequency and the electrical resistance of the magnetic material. The anomalous demagnetization losses are determined by the domain structure of the material.
The hysteresis curve shows an example of the coercive field strength for the static case Hstat (the remagnetization frequency approaches 0 Hz) and the dynamic case H(f). The difference between the dynamic and static coercive field strength determines the excess fieldHexc(f), which is available for the movement of domain walls in the material.
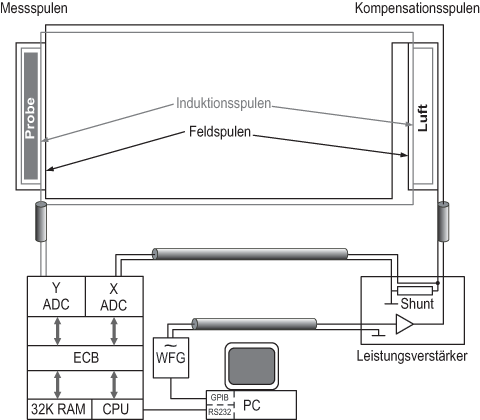
We measure these magnetic properties using a computer-controlled digital hysteresis measurement system.
In the hysteresis measuring system, samples of different dimensions can be measured by adjusting the coil pairs to the specified dimensions. The sample material to be measured is positioned in a coil system consisting of a pick-up coil (induction coil) and a field coil. A similar compensation coil system is connected antiparallel to the measuring coil system. In this way, the vacuum component in the magnetic induction is automatically compensated and the magnetic polarization is measured directly. A programmable frequency generator (WFG) can generate any waveforms of different amplitudes and frequencies up to 15 MHz, which are fed to the coil system as a current signal by a linear amplifying and programmable power amplifier. A correspondingly high magnetic field is generated in the coils. The induction signal of the pick-up coil and the current signal are tapped via a measuring resistor (shunt) and fed to an analog-to-digital converter (ADC) and temporarily stored in RAM. The ADCs digitize the measurement signals with time resolution and are connected via an EC bus to a Z80-based processor that operates autonomously. The hysteresis measuring system communicates with the connected computer (PC) with installed evaluation software via a serial interface (RS232). The shapes and the degree of amplification of the induction signals are controlled using suitably equipped programming boards of the power amplifier. The computer is used to control both the frequency generator (via GPIB) and the Z80 processor for measurement, and once the measurements have been completed, the data is transferred to the PC, which uses special software to determine and evaluate the magnetic characteristics. By optimizing the coils, the measuring system can be adapted to different magnetic materials and sample shapes.
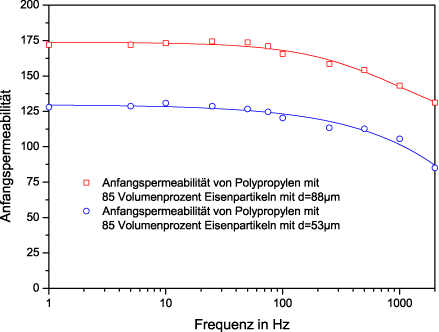
The figure above shows the permeability of two samples made from a polypropylene-iron composite. One composite contains iron particles with an average particle diameter of d=53µm, the other composite has an average particle diameter of d=88µm. The permeability was determined as a function of the remagnetization frequency.
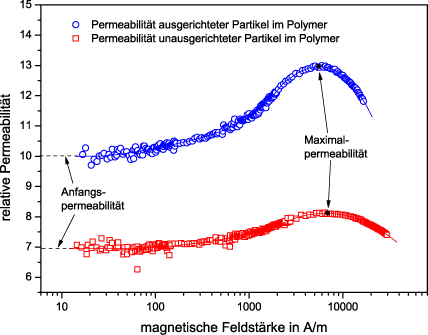
In soft magnetic iron silicon, the magnetic properties are improved by orienting the grains in the material; a pronounced {110} texture (Goss texture) is created in the sheet plane. In polymers filled with soft magnetic particles, the particles can be oriented in the direction of the magnetically light axis of the particles, which also leads to an improvement in the magnetic properties. The image above shows how aligning the magnetic particles in this way leads to a significant increase in permeability.
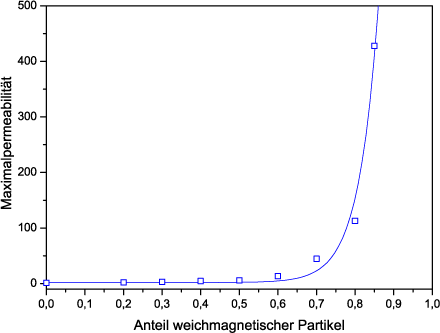
A further significant increase in permeability can be achieved by increasing the proportion of magnetic material in the polymer-magnet composites.
The graph above shows the dependence of permeability on the magnetic content in a polymer. It is easy to see that a significant improvement in permeability can only be achieved with a high proportion of magnetic material. In addition to the measured values, which are represented in the graph by the square symbols, a curve can be seen that runs through the measured values. This curve was calculated on the basis of theoretical considerations and describes the experimental values in good agreement.
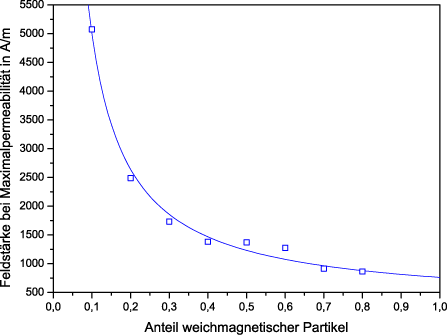
If the proportion of magnetic particles in a polymer is low, a high magnetic field strength is required to achieve the maximum permeability of the material. As the content of magnetic material in the polymer increases, an increasingly lower field strength is sufficient to achieve maximum permeability. This can be seen in the figure below.